বীজগাণিতিক রাশি সূত্রাবলী

বীজগাণিতিক রাশিঃ

প্রক্রিয়া চিহ্ন সংখ্যানির্দেশক অক্ষর প্রতিক এর অর্থবোধক বিন্যাসকে বীজগাণিতিক রাশি বলে । যেমন 2a+3b-4c একটি বীজগাণিতিক রাশি ।

একটি বীজগাণিতিক রাশি তে ধনাত্মক, ঋণাত্ম্‌ গুণ, ভা্‌ সমান চিহ্ন, ইত্যাদি থাকে এবং চলক ও ধ্রুবক থাকে ।

চলক(Variables): বীজগাণিতিক রাশিতে যে উপাদান গুলোর মান নির্দিষ্ট না মান এর পরিবর্তন হয় যেমন উপরের উদাহরনে a , b ও c এদের মানের পরিবতন হয় । তাই এদের চলক বলে ।

ধ্রুবক (Constant) : বীজগাণিতিক রাশিতে ব্যবহৃত সংখ্যাগুলো ধ্রুবক এদের মান নির্দিষ্ট ।

বীজগাণিতিক সূত্রাবলিঃ

বীজগাণিতিক প্রতিক দ্বারা প্রকাশিত যেকোনো সাধারণ নিয়ম বা সিধান্তকে বীজগাণিতিক সুত্র বলা হয় ।

সুত্র ১ । 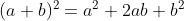$(a+b)^2=a^2+2ab+b^2$

সুত্র ২ । $(a-b)^2=a^2-2ab+b^2$

এই দুটি বর্গের সুত্র থেকে কিছু অনুসিধান্ত প্রমাণ করা যায় যেমনঃ

১ । $a^2+b^2=(a+b)^2-2ab=(a-b)^2+2ab$

২ । $(a+b)^2=(a-b)^2+4ab$ অথবা $(a-b)^2=(a+b)^2-4ab$

সুত্র এক ও দুই থেকে খুব সহজেই এই অনুসিধান্তগুলো প্রমাণ করা যায়

সুত্র ১ থেকে পাই

$(a+b)^2=a^2+b^2+2ab$

বা, $(a+b)^2-2ab=a^2+b^2$

$herefore a^2+b^2=(a+b)^2-2ab$

আবার প্রথম সুত্র থেকে পাই

$(a+b)^2=a^2+2ab+b^2$

বা, $(a+b)^2=a^2+2ab+b^2-2ab+2ab$

বা, $(a+b)^2=a^2-2ab+b^2+4ab$

$herefore$ $(a+b)^2=(a-b)^2+4ab$ ( প্রথম সুত্র থেকে পাই $(a-b)^2=a^2-2ab+b^2$

আবার

অনুসিধান্ত ৩ । $a^2+b^2=frac{(a+b)^2+(a-b)^2}{2}$

প্রমাণঃ

সুত্র ১ ও সুত্র ২ যোগ করি তাহলে

$(a+b)^2+(a-b)^2=a^2+2ab+b^2+a^2-2ab+b^2$

বা, $(a+b)^2+(a-b)^2=2a^2+2b^2$

বা, $2(a^2+b^2)=(a+b)^2+(a-b)^2$

$herefore a^2+b^2=frac{(a+b)^2+(a-b)^2}{2}$

অনুসিধান্ত ৪ । $herefore ab=left (frac{a+b}{2} ight )^2-left ( frac{a-b}{2} ight )^2$

সুত্র ১ ও সুত্র ২ বিয়োগ করে পাই ।

$(a+b)^2-(a-b)^2=a^2+2b+b^2-a^2+2ab-b^2$

বা, $(a+b)^2-(a-b)^2=4ab$

বা, $4ab=(a+b)^2-(a-b)^2$

$herefore ab=left (frac{a+b}{2} ight )^2-left ( frac{a-b}{2} ight )^2$

ঘন সংবলিত সূত্রাবলিঃ

সুত্র ১ । 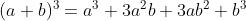$(a+b)^3=a^3+3a^2b+3ab^2+b^3$

সুত্র ২ । $(a-b)^3=a^3-3a^2b+3ab^2-b^3$

সুত্র ১ এর প্রমাণঃ

$(a+b)^3=(a+b)(a+b)^2$

$=(a+b)(a^2+2ab+b^2)$

$=a(a^2+2ab+b^2)+b(a^2+2ab+b^2)$

$=a^3+2a^2b+a^2b+ab^2+2ab^2+b^3$

$=a^3+3a^2b+3ab^2+b^3$

$=a^3+b^3+3ab(a+b)$

সুত্র ২ এর প্রমাণঃ

$(a-b)^3=(a-b)(a-b)^2$

$=(a-b)(a^2-2ab+b^2)$

$=a(a^2-2ab+b^2)-b(a^2-2ab+b^2)$

$=a^3-2a^2b+ab^2-a^2b+2ab^2-b^3$

$=a^3-3a^2b+3ab^2-b^3$

$=a^3-b^3-3ab(a-b)$

অনুসিধান্ত $a^3+b^3=(a+b)(a^2-ab+b^2)$

প্রমাণঃ সুত্র ১ থেকে

$a^3+b^3=(a+b)^3-3ab(a+b)$

$=(a+b){(a+b)^2-3ab}$

$=(a+b)(a^2+2ab+b^2-3ab)$

$=(a+b)(a^2-ab+b^2)$

অনুরূপভাবে $a^3-b^3=(a-b)(a^2+ab+b^2)$

উৎপাদকে বিশ্লেষণঃ

কোনো রাশি দুই বা ততোধিক রাশির গুণফলের সমান হলে, শেষোক্ত রাশিগুলোর প্রথমোক্ত রাশির উৎপাদক বা গুণনীয়ক বলা হয় ।

উৎপাদক নির্ণয়ের কতিপয় কৌশলঃ

ক) কোনো বহুপদীর প্রত্যেক পদে সাধারণ উৎপাদক থাকলে তা প্রথমে বের করে নিতে হয় । যেমনঃ $3a^2b+6ab^2+12a^2b^2=3ab(a+2b+4ab)$

খ) একটি রাশিকে পূর্ণ বর্গ আকারে প্রকাশ করে । যেমন, $4x^2+12x+9$ একটি রাশি

একে বিশ্লেষণ করতে প্রথমে পূর্ণ বর্গ আকারে প্রকাশ করতে হবে ।

$4x^2+12x+9=(2x)^2+2 imes2x imes3+(3)^2$

$=(2x+3)^2=(2x+3)(2x+3)$

গ) একটি রাশিকে দুটি বর্গের অন্তররূপে প্রকাশ করে এবং 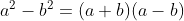$a^2-b^2=(a+b)(a-b)$ সুত্র প্রয়োগ করে ।

ঘ) $x^2+(a+b)x+ab=(x+a)(x+b)$ সূত্রটি ব্যবহার করে ।

এপদ্ধতিতে $x^2+px+1$ আকারের বহুপদীর উৎপাদক নির্ণয় করা সম্ভব হয় যদি দুইটি পূর্ণসংখ্যা a ও b নির্ণয় করা যায় যেন, a + b = p এবং ab=1 হয় । এজন্য q এর দুটি সচিহ্ন উৎপাদক নিতে হয় যাদের বীজগাণিতিক সমষ্টি p হয় । q>0 হলে, a ও b একই চিহ্নযুক্ত হবে এবং q<0 হলে, a ও b বিপরীত চিহ্নযুক্ত হবে ।

ঙ) 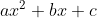$ax^2+bx+c$ আকারের বহুপদীর মধ্যপদ বিভক্তিকরণ পদ্ধতি ।

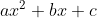$ax^2+bx+c=(rx+p)(sx+q)$ হবে

যদি $ax^2+bx+c=rsx^2+x(rq+sp)+pq$

অর্থাৎ $a=rs,b=rq+sp$ এবং $c=pq$ হয় ।

সুতরাং $ac=rspq=(rq)(sq)$ এবং $b=rq+sq$

অথএব $ax^2+bx+c$ আকারের বহুপদীর উৎপাদক নির্ণয় করতে হলে ac অর্থাৎ 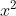$x^2$ এর সহগ এবং x বর্জিত পদের গুনফল্কে এমন দুইটি উৎপাদকে প্রকাশ করতে হবে যাদের বীজগাণিতিক সমষ্টি x এর সহগ b এর সমান হয় ।

জ) ভগ্নাংশযুক্ত রাশির উৎপাদক

ভাগশেষ উপপাদ্য (Remainder, , Theorem):

$6x^2-7x+5$ কে $x-1$ দ্বারা ভাগ করলে ভাগফল হয় $6x-1$ এবং ভাগশেষ হয় $4$

আমরা জানি ভাজ্য = ভাজক $imes$ ভাগফল + ভাগশেষ

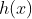এখন যদি আমরা ভাজ্যকে $f(x)$ , ভাগফলকে $h(x)$ , ভাগশেষকে r ও ভাজককে 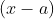$(x-a)$ দ্বারা সূচিত করি, তাহলে উপরের সুত্র থেকে পাই,

$f(x)=(x-a).h(x)+r$ এই সূত্রটি a এর সকল মানের জন্য সত্য ।

উভয়পক্ষে x=a বসিয়ে পাই ,

$f(a)=(a-a).h(a)+r=0.h(a)+r=r$

সুতরাং $r=f(a)$

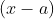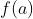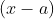অথএব, $f(x)$ কে $(x-a)$ দ্বারা ভাগ করলে ভাগশেষ হয় $f(a)$ . এই সুত্র ভাগশেষ উপপাদ্য নামে পরিচিত । অর্থাৎ ধনাত্মক মাত্রার কোনো বহুপদী $f(x)$ কে $(x-a)$ আকারের বহুপদী দ্বারা ভাগ করলে ভাগশেষ কত হবে তা ভাগ না করে বের করার সুত্রই হল ভাগ শেষ উপপাদ্য । ভাজক বহুপদী $x-a$ আকারের বহুপদী এর মাত্রা 1, ভাজক যদি ভাজ্যের উৎপাদক হয়, তাহলে ভাগশেষ হবে শুন্য । আর যদি উৎপাদক না হয়, তাহলে ভাগশেষ থাকবে এবং তা হবে অশূন্য কোনো সংখ্যা ।

প্রতিজ্ঞাঃ যদি $f(x)$ এর মাত্রা ধনাত্মক হয় এবং $a e0$ হয়, তবে $f(x)$ কে $(ax+b)$ দ্বারা ভাগ করলে ভাগশেষ হয় $fleft ( -frac{b}{a} ight )$

অনুসিধান্তঃ $(x-a),f(x)$ এর উৎপাদক হবে যদি এবং কেবল যদি $f(a)=0$ হয় ।

বাস্তব সমস্যা সমাধানে বীজগাণিতিক সুত্র গঠন ও প্রয়োগঃ

আগের অধ্যায়গুলোতে আমরা যে সুত্র অনুসিধান্ত স্বীকার্য নিয়ে আলোচনা করেছি তাঁর প্রয়োগ করে আমরা এই অধ্যায় এ বিভিন্ন রকম অঙ্ক করব ।

সমস্যা সমাধানের পদ্ধতিঃ

(ক) প্রথমেই সতর্কতার সাথে সমস্যাটি পর্যবেক্ষণ করে এবং মনেযোগ সহকারে পড়ে কোনগুলো অজ্ঞাত এবং কী নির্ণয় করতে হবে তা চিহ্নিত করতে হবে ।

খ) অজ্ঞাত রাশিগুলোর একটিকে যেকোনো চলক ( ধরি x ) দ্বারা সূচিত করতে হবে অতঃপর সমস্যাটি ভালভাবে অনুধাবন করে অন্যান্য অজ্ঞাত রাশিগুলোকে একই চলক x এর মাধ্যমে প্রকাশ করতে হবে ।

গ) সমস্যাকে ক্ষুদ্র ক্ষুদ্র অংশে বিভক্ত করে বীজগাণিতিক রাশি দ্বারা প্রকাশ করতে হবে ।

ঘ) প্রদত্ত শর্ত ব্যবহার করে ক্ষুদ্র ক্ষুদ্র অংশগুলোকে একত্রে একটি সমীকরণে পরকাশ করতে হবে ।

ঙ) সমীকরণটি সমাধান করে অজ্ঞাত রাশি x এর মান নির্ণয় করতে হবে ।

বাস্তব সমস্যা সমাধানে বিভিন্ন সুত্র ব্যবহার করা হয় তা নিচে আলোচনা করা হলোঃ

১) দেয় বা প্রাপ্য বিষয়কঃ দেয় বা প্রাপ্য, A=qn টাকা

যেখানে, q = জনপ্রতি দেয় বা প্রাপ্য টাকার পরিমাণ

n = লোকের সংখ্যা

২) সময় বা কাজ বিষয়কঃ

কয়েকজন লোক একটি কাজ সম্পন্ন করলে কাজের পরিমাণ, $W=qnx$

যেখানে, q = প্রত্যেক একক সময়ে কাজের যে অংশ সম্পন্ন করে,

n = কাজ সম্পাদনকারীর সংখ্যা

x = কাজের মোট সময়

W = n জনে x সময়ে কাজের যে অংশ সম্পন্ন করে ।

৩) সময় ও দূরত্ব বিষয়কঃ

নির্দিষ্ট সময়ে দূরত্ব, d = vt

যেখানে, v = প্রতি ঘণ্টায় গতিবেগ

t = মোট সময়

৪) নল ও চৌবাচ্চা বিষয়কঃ

নির্দিষ্ট সময়ে চউবাচ্চার পানির পরিমাণ $Q(t)=Q_0pm qt$

যেখানে $Q_0=$ নলের মুখ খুলে দেওয়ার সময় চৌবাচ্চায় জমা পানির পরিমাণ

q = প্রতি একক সময়ে নল দিয়ে যে পানি প্রবেশ করে অথবা বের হয় ।

t = অতিক্রান্ত সময়

Q(t)= t সময়ে চৌবাচ্চায় পানির পরিমাণ ( পানি প্রবেশ হওয়ার শর্তে "+" এবং পানি বের হওয়ার শর্তে " - " চিহ্ন ব্যবহার করতে হবে ) ।

৫) শতকরা অংশ বিষয়কঃ

p = br

যেখানে, b = মোট রাশি

r = শতকরা ভগ্নাংশ $=frac{s}{100}=s$ %

p = শতকরা অংশ = b এর s%

৬) লাভ- ক্ষতি বিষয়কঃ

$S=C(Ipm r)$

লাভের ক্ষেত্রে S=C(I+r)

এবং ক্ষতির ক্ষেত্রে, S=C(I-r)

যেখানে, S(টাকা ) = বিক্রয়মূল্য

C(টাকা) = ক্রয়মূল্য

I = লাভ বা মুনাফা

r = লাভ বা ক্ষতির হার

৭) বিনিয়োগ- মুনাফা বিষয়কঃ

সরল মুনাফার ক্ষেত্রে,

I = Pnr টাকা

A = P+I=P+Pnr= P(1+nr) টাকা

চক্রবৃদ্ধি মুনাফার ক্ষেত্রে,

$A=P(1+r)^n$

যেখানে, I= n সময় পরে মুনাফা

n = নির্দিষ্ট সময়

P = মূলধন

r = একক সময়ে একক মূলধনের মুনাফা

A = n সময় পরে মুনাফাসহ মূলধন ।

পৃষ্ঠাসমূহ

শনিবার, ৩ সেপ্টেম্বর, ২০১৬