অনুপাত ও সমানুপাতের ধর্মঃ
[ বি দ্রঃ নিচের অনুপাত ও সমানুপাতের ধর্মগুলো মনে রাখতে হবে নিচের ধর্মগুলো মনে না রেখে এই অধ্যায়ের কোনো অঙ্ক না করার পরামর্শ দেওয়া হলো নিচের ধর্মগুলো মনে রাখলে অঙ্কগুলো অনেক সহজ হবে ]
(i) a : b =x : y এবং c : d = x : y হলে, a : b = c : d
(ii) a : b=b : a হলে , a = b
(iii) a : b = x: y হলে, b : a = y :x ( ব্যস্তকরন )
(iv) a : b = x : y হলে, a : b = b : y (একান্তরকরন )
(v) a : b = x : y হলে ad = bc (আড়গুণন )
(vi) a : b=x : y হলে, a+b : b = x+y : y (যোজন )
এবং a-b : b = x-y : y ( বিয়োজন )
(vii)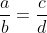 
হলে, 
( যোজন বিয়োজন )
হলে, ( যোজন বিয়োজন ) জ্যমিতিক অনুপাতঃ
ত্রিভুজের ক্ষেত্রফলের ধারণা থেকে দুইটি প্রয়োজনীয় অনুপাতের ধারণা পাওয়া যায় ।
১) দুইটি ত্রিভুজক্ষেত্রের উচ্চতা সমান হলে তাদের ক্ষেত্রফল ও ভূমি সমানুপাতিক ।
মনে করি ত্রিভুজক্ষেত্র ABC ও DEF এর ভূমি যথাক্রমে BC=a EF= d এবং উভয় ক্ষেত্রের উচ্চতা h । সুতরাং ABC এর ক্ষেত্রফল 
ত্রিভুজক্ষেত্র DEF এর ক্ষেত্রফল 
ত্রিভুজক্ষেত্র DEF এর ক্ষেত্রফল 
অথএব ত্রিভুজক্ষেত্র ABC এর ক্ষেত্রফলঃ ত্রিভুজ ক্ষেত্র DEF এর ক্ষেত্রফল 
২) দুইটি ত্রিভুজক্ষেত্রের ভূমি সমান হলে তাদের ক্ষেত্রফল ও উচ্চতা সমানুপাতিক ।
মনে করি ত্রিভুজক্ষেত্র ABC ও DEF এর উচ্চতা যথাক্রমে AP = h, DQ = k এবং উভয়ক্ষেত্রের ভূমি b ।
সুতরাং, ত্রিভুজক্ষেত্র ABC এর ক্ষেত্রফল 
, ত্রিভুজক্ষেত্র DEF এর ক্ষেত্রফল 
, ত্রিভুজক্ষেত্র DEF এর ক্ষেত্রফল 
কোন মন্তব্য নেই:
একটি মন্তব্য পোস্ট করুন