শনিবার, ৩ সেপ্টেম্বর, ২০১৬

দুই চলকবিশিষ্ট সরল সহসমীকরন | নবম-দশম শ্রেনী

সরল সমীকরণঃ

সরল সমীকরণ বলতে দুই চলকবিশিষ্ট সরল সমীকরণকে বোঝায় যখন তাদের একত্রে উপস্থাপন করা হয় এবং চলক দুইটি একই বৈশিষ্ট্য এর হয় । আবার এরূপ দুইটি সমীকরণকে একত্রে সরল সমীকরণজোটও বলে । 

দুই চলকবিশিষ্ট সরল সহসমীকরণের সমাধান যোগ্যতাঃ

সঙ্গতিপূর্ণ ও পরস্পর অনির্ভরশীল সমীকরণজোটের ক্ষেত্রে ধ্রুবপদের অনুপাতগুলো সমান না । 

প্রতিস্থাপন পদ্ধতিতে সমাধানঃ

সুবিধামত একটি সমীকরণ থেকে একটি চলকের মান অপর চলকের মাধ্যমে প্রকাশ করে প্রাপ্ত মান অপর সমীকরণে বসালে এক চলকবিশিষ্ট স্মিকরন পাওয়া যায় । অতঃপর সমীকরণটি সমাধান করে চলক্তির মান পাওয়া যায় । এই মান প্রদত্ত সমীকরণের যে কোনটিতে বসানো জেতে পারে । তবে যেখানে একটি চলককে অপর চলকের মাধ্যমে প্রকাশ করা হয়েছে সেখানে বসালে সমাধান সহজ হয় । এখানে অপর চলকের মান পাওয়া যায় । 


অপনয়ন পদ্ধতিতে সমাধানঃ

সুবিধামত একটি সমীকরণকে বা উভয় সমীকরণকে এরূপ সংখ্যা দিয়ে গুণ করতে হবে যেন গুণনের পর উভয় সমীকরণের যেকোনো একটি চলকের সহগের পরমমান সমান হয় । এরপর প্রয়োজনমত সমীকরণ দুইটিকে যোগ বা বিয়োগ করলে সহগ সমানকৃত চলকটি অপনীত বা অপসারিত হয় । তারপর সমীকরণটি সমাধান ক্করলে বিদ্যমান চলকটির ,মান পাওয়া যায় । ঐ মান সুবিধামত প্রদত্ত সমীকরণদ্বয়ের যেকোনোটিতে বসালে অপর চলকটির মান পাওয়া যায় । 
গাণিতিক প্রকাশ নিম্নে দেওয়া হলোঃ
নিচের সমীকরণ দুইটি বিবেচনা করিঃ
a_{1}x+b_{1}y+c_{1}=0..................(i)
a_{2}x+b_{2}y+c_{2}=0..................(ii)
[এখানে a_{1},b_{1},c_{1}, a_{2},b_{2},c_{2} ধ্রুবপদ এদের মান যেকোনো কিছু হতে পারে যেমন, 1,2,3,4,5,........ ইত্যাদি ]
সমীকরণ (i) কে 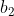b_{2} দিয়ে এবং সমীকরণ (ii) কে 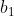b_{1} দিয়ে গুণ করে পাই, 
a_{1}b_{2}x+b_{1}b_{2}y+b_{2}c_{1}=0...........(iii)
a_{2}b_{1}x+b_{2}b_{1}y+b_{1}c_{2}=0...........(iv)
সমীকরণ (iii) থেকে (iv) বিয়োগ করি 
(a_{1}b_{2}-a_{2}b_{1})x+b_{2}c_{1}-b_{1}c_{2}=0
বা, (a_{1}b_{2}-a_{2}b_{1})x=b_{1}c_{2}-b_{2}c_{1}
বা, frac{x}{b_{1}c_{2}-b_{2}c_{1}}=frac{1}{a_{1}b_{2}-a_{2}b_{1}}...............(v)
আবার সমীকরণ (i) কে 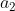a_2 দিয়ে ও সমীকরণ (ii) কে 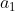a_1 দিয়ে গুণ করে পাই, 
a_{1}a_{2}x+b_{1}a_{2}y+a_{2}c_{1}=0......................(vi)
a_{1}a_{2}x+a_{1}b_{2}y+a_{1}c_{2}=0                     (vii)
সমীকরণ (vi) থেকে সমীকরণ (vii) বিয়োগ করে পাই,
(a_{2}b_{1}-a_{1}b_{2})y+c_{1}a_2-c_2a_1=0
বা, (a_{2}b_{1}-a_{1}b_{2})y=c_2a_1-c_{1}a_2
বা, frac{y}{c_{1}a_2-c_2a_1}=frac{1}{a_{1}b_{2}-a_{2}b_{1}}............(viii)
সমীকরণ (v) ও (viii) থেকে পাই 
frac{x}{b_1c_2-b_2c_1}=frac{y}{c_{1}a_2-c_2a_1}=frac{1}{a_{1}b_{2}-a_{2}b_{1}}
[ বি দ্রঃ বহুনির্বাচনী প্রশ্নের উত্তরের জন্য এই সুত্রটি মনে রাখা দরকার 
{color{Red} frac{x}{b_1c_2-b_2c_1}=frac{y}{c_{1}a_2-c_2a_1}=frac{1}{a_{1}b_{2}-a_{2}b_{1}}}   ]

লৈখিক পদ্ধতিতে সমাধানঃ

যদি x ও y এর মান উভয়ই ধনাত্মক হয় তাহলে বিন্দুটি লেখচিত্রের প্রথম চতুর্থভাগে থাকবে যদি x এর মান ঋণাত্মক এবং y এর মান ধনাত্মক হয় তাহলে বিন্দুটি দ্বিতীয় চতুর্থভাগে থাকবে যদি x এর মান ধনাত্মক এবং y এর মান ঋণাত্মক হয় তাহলে বিন্দুটি চতুর্থ চতুর্থভাগে থাকবে এবং যদি x ও y উভয়ের মান এ ঋণাত্মক হয় তাহলে বিন্দুটি তৃতীয় চতুর্থভাগে অবস্থিত হবে । 

বাস্তব ভিত্তিক সমস্যা

বাস্তব ভিত্তিক সমস্যার সমীকরণ গঠন ও সমাধান ।
ট্যাগসমূহ:

কোন মন্তব্য নেই:

একটি মন্তব্য পোস্ট করুন

Related Posts Plugin for WordPress, Blogger...